1. Introduction to Probability:
Probability involves the study and measurement of uncertainty (uncertain events) and the risk associated to it. Probability is the expression of likelihood of occurrence of particular event. Probability of occurrence of particular event can be measured in between 0 and 1. Zero for an event which cannot occur and one for an event which is certain to occur. Uncertainty such as future demand, future sales, future supplies, future interest rate, and future inflation all are common factors in business and management. Therefore, we can conclude that all our present decisions are influenced and impacted by future uncertain events. Finally, we can say that in order to make sound decision we should try to deal with future uncertainty in systematic manner using the theory of probability. In one sentence we can say that probability is Chance of/ Likely to / Likelihood of happening or occurring of an event. These days the probability theory has become one of the most important basic tools in statistics. Every managerial decision either based on past experience or on informed guess that is subjective probability. Hence, theory of probability plays vital role in today’s competitive business as it provides the numerical measures for the uncertainty. Before we introduce the probability theory, we will discuss a special counting principles/rules, permutations and combination, which are used in computing probabilities.
2. Counting Rules / Principles in Probability:
Especially in probability we use two types of counting principles, that is, principles of multiplication and principle of addition. These two counting principles are highly used in probability in order to compute total number of permutations and combinations.
2.1. Principle of Multiplication:
If an event X can occur in m ways and if following it, a second event can occur in n ways, and then the two events X and Y in succession can occur in m X n ways.
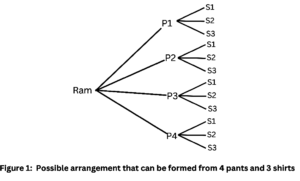
For example: suppose Ram has 4 pants of different colors and 3 shirts of different colors, in how many different ways can he wear these pants and shirts both? The total number of ways that he can wear these pants and shirts are equal to: 4×3=12 ways. The following figure represents the possible arrangements.
2.2. Principle of Addition:
If two events A and B do not occur simultaneously and if the first event occurs in m different ways and second n different ways, then one or other occur in (m+n) ways. For example: let there are 5 bus routes and 3 train route between two cities. A person can go from city X to Y by any one of the bus routes or any one of the train routes. Thus, there are 5+3=8 ways by which the person can travel from one city to another city.
3. Permutation and Combination:
Permutation and combination are two major aspect of statistics based on counting principles. Permutation and combination deal with the arrangement and selection of objects in particular manner. Before using permutation and combination we must understand the concept and difference between permutation and combination.
3.1. Permutation:
Permutation is the process of arranging available objects in a specific sequence or order and forming their subset. Permutation considers the sequence or order of elements. For example, in permutation (A, B) and (B, A) are distinct set of objects as their order is different even the elements are same. Permutations can be of two types:
a) Linear Permutation
b) Circular Permutation
a) Linear Permutation:
Linear permutation refers to the sequential arrangement of objects in a line. It is of four types which are as under:
i) Permutation without Repetition
ii) Permutation with Repetition
iii) Permutation of Multi Sets / Distinguishable Permutation
iv) Restricted / Conditional Permutation
i) Permutation without Repetition:
It is the permutation of n different objects taken all or r objects at a time when repetition is not allowed.
In this type of selection, our choices reduce every time. For example: What order could 52 playing cards be in?
In this case first we have 52 possibilities but after first choice we have only 51 possibilities for next choice, then after choices will be continuously reduces to 50, 59, 48, 47 etc. In this case total permutations taking r items at a time from n objects without repetition [nPr or nPr or P(n,r)] can be given as:
nPr= n(n-1) (n-2) (n-3)……………(n-r+1), where n is positive integer, r is whole number and r<n. Hence total permutations in the above case = 52x51x50x49x48….=311,857,200.
Formula for Permutation without Repetition \((^{n}P_{r})= \frac{n!}{(n-r)!}\)
Sometimes when r = n (taken all at a time) then number of permutations \((^{n}P_{r})= \frac{n!}{(n-r)!}\)
= \(\frac{n!}{(n-n)!}\)
= \(\frac{n!}{0!}\)
=\(\frac{n!}{1}\)
=\(n!\)
Where, ! is a factorial notation and mathematically 0! is equal 1. I order to make certain formula valid in all cases factorial zero is arbitrarily defined to be 1. Factorials of proper fractions or negative integers are not defined. Factorial n is defined only for whole numbers. Sometimes n! is also represented by Ln.
Factorial Notation:
Factorial notation refers to the mathematical operation of multiplying a number by all the positive whole numbers less than itself. This is represented by an exclamation mark after the number, for example, 5! means 5 x 4 x 3 x 2 x 1 = 120.
Factorial notation is commonly used in probability theory, combinatorics, and statistics. It can also be used to express the number of ways in which a set of items can be arranged. For instance, the number of different ways in which six people can arrange themselves in a line can be expressed as 6!
Understanding factorial notation can be beneficial for solving various mathematical problems, especially in the fields of science, technology, engineering, and mathematics. Hence, it is essential for students and professionals to have a firm grasp of this concept. With its widespread use, mastering factorial notation can help individuals in various dimensions of life.
ii) Permutation with Repetition:
It is the permutation of n different objects taken all or r objects at a time when repetition is allowed.
In this case our choices remain constant every time and are equivalent to total number of objects (n). Hence drawing r items from n items with repetition can be given as:
nPr = nxnxn…….upto r times = nr where n is positive integer, r is whole number and r<n.
Example: Find the number of 3 letter words that can be formed from the letters a, e, i, o, and u in which letter are allowed to be repeated.
Here,
Total number of letter (n) = 5
Number of letters in each word (r) = 3
No. of Permutations with Repetition (nPr) = nr = 53 = 125
iii) Permutation of Multi Sets / Distinguishable Permutation:
It is the case where all the n elements are not different but some of them are similar. In this situation, the number of permutations of n objects taken all at a time, when t1 objects are of one type, t2 objects are of second type, t3 objects are of third types and tn objects are of another types then total number of possible permutations can be \((^{n}P_{r})= \frac{n!}{t_1!\times t_2!\times t_3!\times…….t_n!}\).
For Example: Find the total number of permutations of letters in the word “STATISTICS”. Here, all the letters in “STATISTICS” are not different, some of them are alike. Hence,
Total Number of Letters (n) = 10
Number of letter “T” = 3
Number of letter “S” = 3
Number of letter “I” = 2
Number of letter “A” = 1
Number of letter “C” = 1
Possible numbers of permutations (nPr)
= \(\frac{n!} {T!\times S!\times I!\times A!\times C!}\)
= \(\frac{10!} {3!\times 3!\times 2!\times 1!\times 1!}\)
= 50,400
iv) Restricted/ Conditional Permutation:
Restricted permutation is a way of filtering and selecting a set of objects by imposing certain constraint in the sequence of selection. In this type of permutation arrangement of object can be restricted by fixing the position of particular objects in the given set, including or excluding the certain objects in the given set and the like. Three major cases of restricted permutation can be explained as under:
a) Permutations Restricted by Fixed Position or Place of Objects
b) Permutations Restricted by Complete Exclusion and Inclusion of some objects
C) Permutations Restricted by Togetherness and Separation of some Objects
a) Permutations Restricted by Fixed Position or Place of Objects
i) The number of permutations of n different objects taken r at a time, when a particular thing occupies fixed (definite) position can be given as: n-1Pr-1.
ii) The number of permutations of n different objects taken all at a time when m number of objects occupy fixed (definite) position can be given as: m! x (n-m)!.
Example: How many words can be formed with the letters of word “MANGO” when:
i) “M” and “O” occupying end places.
Here,
Total Objects (n) = 5
Number of Fixed Object (m) = 2, i.e. “M” and “O” fixed at end places
Object Drawing Per Time (r) = Total Number of Object (n), i.e. all at a time.
Possible Number of Permutations when Objects are fixed = m! x (n-m)!
= 2! x (5-2)!
= 2! x 3!
=2x1x3x2x1
= 12 ways
ii) “N” always occupying middle places.
Here,
Total Objects (n) = 5
Number of Fixed Object (m) = 1, i.e. letter “N” is fixed at middle position
Object Drawing Per Time (r) = Total Number of Object (n), i.e. all at a time.
Possible Number of Permutations when Objects are fixed = m! x (n-m)!
= 1! x (5-1)!
= 1! x 4!
=4x3x2x1
= 24 ways
b) Permutations Restricted by Complete Exclusion and Inclusion of some objects
i) The number of permutations of n different objects taken r at a time when m particular things are always excluded (not taken/ never occur) can be given as: n-mPr.
ii) The number of permutations of n objects taking r at a time where m particular things always occurred is given as: n-mCr-m × r! or r× n-mPr-m or r x \(\frac{(n-m)!}{(r-m)!}\)
Example: In how many ways the word “MANGO” can be arranged taken 3 letters at a time, when 2 particular letters never occur?
Here,
Total Number of Letters (Objects) (n) = 5
Number of Letters Drawing at a time (r) = 3
Number of Letters Never Occur (m) = 2
Required Number of Arrangement (Permutations) when 2 particular letters never occur = n-mPr.
= \(^{5-2}P_{3}\)
= \(\frac{3!}{(3-3)!}\)
= \(\frac{3!}{(0)!}\)
= 3 x 2 x1
= 6 ways
Example: Determine how many 4 digits numbers without any repetition can be made using 1,2,3,4,5,6,7 if 4 will always be there in the number.
Here,
Total Number of Objects (n) = 7
Number of Drawing at a time (r) = 4
Number of Objects that must be in every arrangement (m) = 1 i.e., number 4 must be there in every arrangement
Now,
Possible Number of Permutations = n-mCr-m × r! or r× n-mPr-m or r x \(\frac{(n-m)!}{(r-m)!}\) use any one out of these three formula.
= r x \(\frac{(n-m)!}{(r-m)!}\)
= 4 x \(\frac{(7-1)!}{(4-1)!}\)
= 4 x \(\frac{6!}{3!}\)
= 4 x \(\frac{6x5x4x3x2x1}{3x2x1}\)
= 480 different arrangements can be made
C) Permutations Restricted by Togetherness and Separation of some Objects:
i) The number of permutations of n different things taken all at a time when m specified objects always come together is given as: (n-m+1)!×m!.
ii) The number of permutations of n different objects taken all at a time when m specified objects never come together is given as: n!-(n-m+1)!×m!.
Example: How many words can be formed with the letters of the word “OMEGA” when vowel being never together?
Here,
Number of Letters (n) = 5
Number of Vowel (m) =3 i.e. O, E, and A
Possible Number of Permutations (if vowels never come together) = n!-(n-m+1)!×m!. (taking all at a time)
= 5! – (5-3+1)! x 3!
= 5x4x3x2x1 -3!x3!
=120 – 3x2x1x3x2x1
= 120 – 36
= 84 words can be formed.
Example: How many words can be formed with the letters of the word “OMEGA” when vowel are always together?
Here,
Number of Letters (n) = 5
Number of Vowel (m) =3 i.e. O, E, and A
Possible Number of Permutations (if vowels are always together) = (n-m+1)!×m!. (taking all at a time)
= (5-3+1)! x 3!
= 3!x3!
=3x2x1x3x2x1
= 36
= 36 words can be formed.
b) Circular/ Cyclic Permutation:
Circular permutations are the arrangement of objects in a circular manner. In linear permutations, there is always starting and ending points but in circular permutation, there is neither starting point nor ending point. Therefore, in circular permutation we have to keep one of the objects fixed and remaining objects are to be arranged. First element has only one choice in circular permutation. Therefore, possible number of permutations under circular arrangement can be computed as under:
a. Number of circular permutations of “n” different objects taking all at a time when
i) Clockwise and anticlockwise orders are different = (n-1)!
ii) Clockwise and anticlockwise orders are same = (n-1)!/2
b. Number of circular permutations of “n” different objects taking “r” at a time when
i) Clockwise and anticlockwise orders are different = nPr/r
ii) Clockwise and anticlockwise orders are same = nPr/2r
c. Other Important Formulae Related to Circular (Cyclic) Permutation
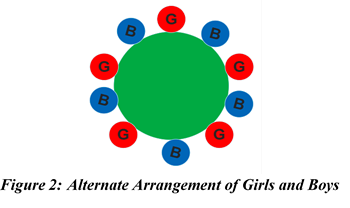
Example 1: In how many ways 5 girls and 5 boys can be arranged in a circle if:
i) There is no Restriction.
ii) Boys and Girls be Alternate (restricted or conditional case)
iii) Boys and Girls are in the form of couples (restricted or conditional case)
iv) Boys and Girls are Separate (restricted or conditional case)
v) One of the couples got Breakup (restricted or conditional case)
i) There is no Restriction
Here,
Total Number of Objects or Elements (n) = 10 (5 girls and 5 boys)
Total Number of Possible Arrangement (Permutation) = (n-1)!
= (10-1)!
= 9!
= 9x8x7x6x5x4x3x2x1
= 362,880 ways
ii) Boys and Girls be Alternate (restricted or conditional case)
We know this is restricted or conditional case of permutation (arrangement) where elements of two groups should be in alternate position (no two elements of any group come together). When the case is conditional or restricted, we have to handle or arrange elements in groups or group separately. In such cases it is rationale to arrange elements in free (unconditional / unrestricted) group firstly and then secondly, we have manage elements in restricted group as per available places for them.”
In this case boys have fixed five (m) places to seat and girls have five (n) fixed places to seat. Here, either girls need to follow the given condition or boys need to follow the given condition. One of them is free and one of them needs to follow condition.
Now,
Possible Number of Permutation (ways / arrangement) = Circular Permutations of Free Objects (Boys) x Linear Permutations of Restricted Objects (Girls)
= (m-1)! x nPn.
= (5-1)! x n!
= 4! x 5!
= 4x3x2x1x5x4x3x2x1
= 2,880 ways
iii) Boys and Girls are in the form of Couples (restricted or conditional case)
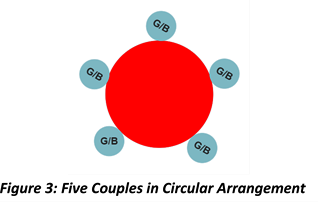
In this case, we can form 5 couples from 5 boys and 5 girls as shown in figure 3 above. Each couple should be considered as single object or single unit. Hence, in this case we need to arrange 5 couples in circular form. Here we also consider the permutations of internal objects that is, girls and boys in each group. Therefore,
Here,
Total Number of Couples or Objects (n) = 5
Numbers of Members or Objects within each Couple (m) = 2 (each group has 2 members, that is , a girl and a boy)
Total Number of Permutation = Circular Permutation of 5 Couples x Linear Permutations of Members within each Couples
\(=(n-1)! \times ({^{m}P_{m}})^{n}\)
\(=(5-1)! \times ({^{2}P_{2}})^{5}\)
\(= 4! \times {(2)^5}\)
\(= 4 \times 3\times 2\times 1\times {(2)^5}\)
\(= 768 \) ways
iv) Boys and Girls are Separate (restricted or conditional case)

By separating girls and boys, we can create two groups- one group consisting of five girls and another group consisting of five boys, as demonstrated in above Figure 4. Therefore, in this case, Therefore, in this case,
Total Number of Objects or Groups (n) = 2
Number of Objects or Elements in each Group (m) = 5
Now,
Total Number of Permutations = Circular Permutations of two Groups x Linear Permutation of Objects within each Groups
\(=(n-1)!\times (^{m}P_{m})^{n}\)
\(=(2-1)!\times (^{5}P_{5})^{2}\)
\(=1!\times {(5!)^2}\)
\(=1\times {(5\times 4\times 3\times 2\times 1)}^2\)
\(=(120)^2\)
\(=14,400\) ways
v) Breakup of one couple (restricted or conditional case)
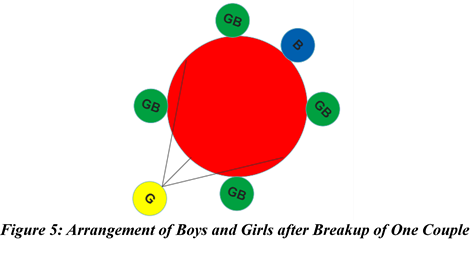
In the event of a couple splitting up, six individuals will be involved: four couples, one male, and one female. In this case, we have to decide whether to fix the position of the male or the female partner from the separated couple. Having made that decision, we then organize the four remaining couples and the individual from the separated couple. For this example, we have chosen to keep the male partner from the separated couple in a fixed position. This approach allows the female partner from the separated couple to select from three available seats as shown above in figure 5.
Here,
Total Possible Number of Permutation = Circular Permutation of Fixed Object (Breakup Boy) x Linear Permutation of Four Couples x Linear Permutations of Objects within Four Couples x Linear Permutations of Breakup Girl
Now,
Circular Permutation of Fixed Object (Breakup Boy) = (n-1)! = (1-1)! = 0! = 1 ways
Linear Permutation of Four Couples = nPn = n! = 4! = 4x3x2x1 = 24 ways
Linear Permutations of Objects within Four Couples = (2!)4 = 16 ways (Note: 2 members in each couple can be arranged in two ways and there are 4 couples.)
Linear Permutations of Breakup Girl = Breakup Girl has 3 choices (places) to seat = nPr = 3P1 = \(\frac{3!} {2!}\) = 3 ways
Now as per multiplication rule of counting,
Total Number of Possible Permutation = 1x24x16x3 = 1,152 ways
Example 2: Out of 10 flowers of different colors, how many different colors, how many different garlands can be made if each garland consists of 6 different flowers ?
Here,
Note: In the case of garland, there is no difference between clockwise and anticlockwise orders.
In this case,
Number of circular permutation of “n” different objects taking “r” at a time can be: \(\frac{^nP_r} {2r}\)
Therefore, in this case
Total Number of Objects (n) = 10
Number of Selected Objects (r) = 6
Total Number of Arrangement (Permutation) = \(\frac{^nP_r} {2r}\)
\(=\frac{^nP_r} {2r}\)
\(=\frac{^{10}P_{6}} {(2\times 6)}\)
\(=\frac{\frac{10!}{4!}} {12}\)
\(=\frac{\frac{(10\times 9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1)}{(4\times 3\times 2\times 1)}} {12}\)
\(=12,600\) ways
Example 3: In how many ways 6 person can sit at a round table, if two of them prefer to sit together?
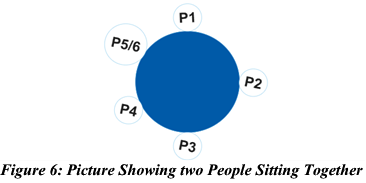
Figure 6 illustrates six individuals (P1, P2, …., P6), among whom two individuals (P5 and P6) are seated together. When two individuals (P5 and P6) sit together as a group, we should consider them as a single unit. Therefore, in this scenario
Total Number of Objects (n) = 5
Total Objects within Group (m) = 2
Now,
Total Number of Possible Arrangement = Circular Permutation of Total (n) Objects x Linear Permutation of Objects (m) within each Group
\(= (n-1)!\times {^mP_m}\)
\(= (5-1)!\times {^2P_2}\)
\(= 4!\times 2!\)
\(= 4\times 3\times 2\times 1\times 2\times 1\)
\(=48\) Ways
Example 4: In how many ways the letters of the word “MONDAY” can be written around a circle if the vowels are to be separated in any arrangement ?
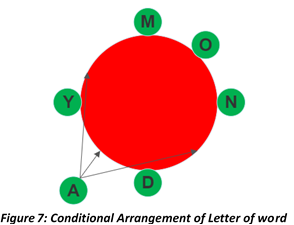
Here, we have a set of 6 objects. Out of 6 objects, 4 (M, N, D, and Y) are free objects that can be arranged in any order, while 2 objects, “O” and “A”, are bound by a condition that they must be separated in any arrangement. Our task is to arrange the 4 free objects and then fix either “A” or “O” in a specific position. Specifically, we have chosen to fix “O” between “M” and “N” as shown in above figure 7. Now, we have three possible position for “A” to be placed.
Now,
Number of Fixed Object (n) = 1 (“O”)
Number of Consonant (m) = 4 (M, N, D, & Y)
Number of Free Vowel (r) = 1 (“A”)
Available Places for “A” (q) = 3
Here,
Possible Number of Permutation = Circular Permutation of Fixed Object (O) x Linear Permutation of Consonant (M, N, D, & Y) x Linear Permutation of Vowel (A)
\(Possible Number of Permutation = (n-1)!\times ^mP_m\times ^qP_r\)
\(= (1-1)!\times m!\times ^3P_1\)
\( = 0!\times 4!\times \frac {3!} {2!}\)
\( = 1\times 4\times 3\times 2\times 1\times \frac {3\times 2\times 1} {2\times 1}\)
\(=72\) ways
Alternatively
Here, we can categorize total objects into two group, that is, unrestricted group (m = consonant) and restricted group (n = vowel)
Objects in unrestricted group (m) = 4 (M, N, D, & Y)
Objects in restricted group (n) = 2 (A, & O)
The number of circular permutations of “m” things of first kind and “n” things of second kind where no two things of second kind come together is
\(=(m-1)!\times ^mP_n\)
\(=(4-1)!\times ^4P_2\)
\(=3!\times \frac {4!}{2!}\)
\(=3\times 2\times 1\times \frac {4\times 3\times 2\times 1}{2\times 1}\)
\(=72\) ways
Example 5: In how many ways we can form a garland using 3 different red flowers, 5 different yellow flowers, and 4 different blue flowers, if flowers of same color must be together?
Solution:
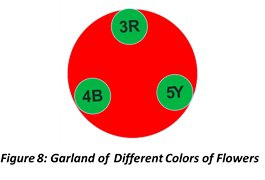
Here, as per the condition provided, yellow, red, and blue flower in garland must be in group of same color as shown in figure 8. Hence, we can consider each group as a single unit. Therefore,
Total Number of Object (n) = 3
Number of yellow flowers (y) = 5
Number of red flowers (r) = 3
Number of blue flowers (b) = 4
Now,
Total Number of Permutations = Circular Permutation of Overall Group x Linear Permutations Objects in Each Group (Red Flower Group, Blue Flower Group, and Yellow Flower Group)
= Circular Permutation of Overall Group x Linear Permutation of Red Flowers x Linear Permutation of Blue Flowers x Linear Permutation of Yellow Flowers
\(=(n-1)!\times ^yP_y\times ^rP_r\times ^bP_b\)
\(=(3-1)!\times ^5P_5\times ^3P_3\times ^4P_4\)
\(=2!\times 5!\times 3!\times 4!\)
\(=2\times 1\times 5\times 4\times 3\times 2\times 1\times 3\times 2\times 4\times 3\times 2\times 1\)
\(=34,560\) ways
Note: In the above case types of flower is different, hence clockwise and anticlockwise orders are different here.
Example 7: In how many ways the letter in word “TERRORISM” can be arrange in a circle?
Solution:
Here,
Total Number of Object (n) = 9
Number or Repeated (alike) Object (p) = 3
Number of circular permutation when objects are alike (repeated) can be given as: \(\frac{(n-1)!}{p!\times q!\times r!}\)
Therefore,
Total Number of Circular Permutation =\(\frac{(n-1)!}{p!}\)
\(=\frac{(9-1)!}{3!}\)
\(=\frac{8!}{3!}\)
\(=\frac{8\times 7\times 6\times 5\times 4\times 3\times 2\times 1}{3\times 2\times 1}\)
\(=6,720\) ways
Other Important Problems with Restrictions (Conditional Cases)
Case I: When certain type (category) of things comes together
Example: In how many ways 5 science books, 4 mathematics books, and 6 English books can be arranged, so that books of same subjects are always together.
Solution:

Here each type of book can be considered as 1 unit or 1 object. Therefore, in this case, we have to arrange 3 broad category or group (type) in three different places. Secondly, we have to arrange different number of elements (objects) in each group individually. Hence, in this case
Total Number of Group (n) = 3 (Science, Mathematics, & English)
Number of Science Books (s) = 5
Number of Mathematics Books (m) = 4
Number of English Books (e) = 6
Now,
Required Number of Arrangement or Permutation (P) = Linear Arrangement of Overall Groups x Linear Arrangement of Elements in Each Group
=3 group can be arranged in 3 ways (nPn) x 5 Science books can be arranged in 5 ways (sPs) x 4 mathematics books can be arranged in 4 ways (mPm) x 6 English books can be arranged in 6 ways (ePe)
\(= (^nP_n)\times (^sP_s)\times (^mP_m)\times (^eP_e)\)
\(= n!\times s!\times m!\times e!\)
\(= 3!\times 5!\times 4!\times 6!\)
\(= 3\times 2\times 1\times 5\times 4\times 3\times 2\times 1\times 4\times 3\times 2\times 1\times 6\times 5\times 4\times 3\times 2\times\)
\(=12,441,600\) ways
Case II: When two different type of objects never come together